Tijd over om je te verbeteren, om je kennis te verbreden in bijvoorbeeld programmeren? Ga aan de slag met eenvoudige uitdagingen en neem een spelletje en kijk eens hoe je dit kunt omzetten naar een paar regels VBA code. Door hele eenvoudige problemen te nemen als "project" kun je je helemaal op het programmeren richten en niet zo zeer op de werking van het spel. Neem bijvoorbeeld Boter-Kaas-En-Eieren of Sudoku en ga aan de slag, automatiseer de oplossing.



Een Sudoku
Iedereen heeft wel eens een Sudoku gezien of zelf ter hand genomen. Het is een snel en relatief eenvoudig cijfer puzzeltje. Je komt ze ook overal tegen, in kranten, tijdschriften en in de app-store. Je kunt altijd snel en overal een Sukoku oplossen.
Hier even kort de spelregels (figuren van links naar rechts en van boven naar beneden):
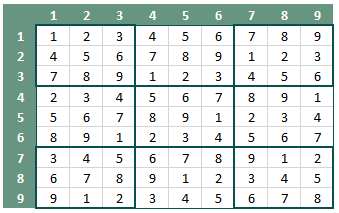
- Er is een speelveld van 9x9 vlakjes, waarbij 9 vlakken worden gevormd van 3x3 vlakjes (figuur 1).
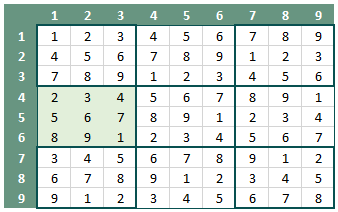
- In elke rij moeten de cijfers 1 t/m 9 worden ingevuld (figuur 2 - rij 2).
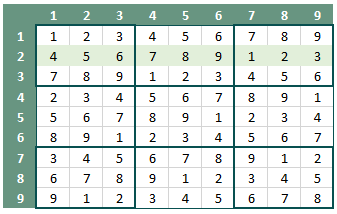
- In elke kolom moeten de cijfers 1 t/m 9 worden ingevuld (figuur 3 - kolom 2).
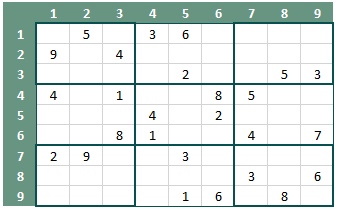
- In ieder veldje 3x3 moeten de cijfers 1 t/m 9 worden ingevuld (figuur 4 - veld [4,1] t/m [6,3])
- In één rij, één kolom én één veldje mogen geen dubbelingen voorkomen. Elk getal mag maar één keer worden gebruikt in een rij, kolom en veldje.
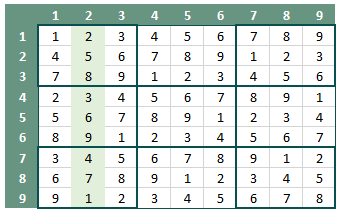
- Elke Sudoku start met een aantal hints. Dit zijn vlakjes die reeds zijn ingevuld. De stelling is, hoe meer hints zijn ingevuld hoe makkelijker de Sudoku kan worden opgelost (figuur 5).
- Als we deze regels volgen komen we voor Sudoku (5) tot de oplossing zoals weergegeven in figuur 6.
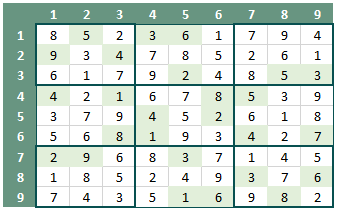
Het mooie van Sudoku is dat het eigenlijk onmogelijk is dat je ooit dezelfde Sudoku twee keer speelt. Er zijn maar liefst 6.670.903.752.021.072.936.960 verschillende unieke Sodoku's.
Meer hints vereenvoudigd de puzzel en minder hints maakt een puzzel dus moeilijker. Maar wat is dan het minimaal aantal hints nodig om een Sudoku op te lossen. Recent is hier, na een hele lange zoektocht, een wiskundige oplossing voor gevonden. Het minimaal aantal benodigde hints is 17 stuks.
Hoe kunnen we VBA gebruiken voor het oplossen van een Sudoku?
Wat we eerst moeten doen, is het probleem analyseren. Hoe pakken we dit aan? Zet de verschillende stappen eens op papier. Je zult zien dat de benodigde stapjes snel naar voren komen en het aantal stapjes is beperkt én zijn relatief eenvoudig. Ideaal dus voor een oefening VBA programmeren.
De stappen:
- Zoek een leeg veldje in de puzzel.
Begin bijvoorbeeld moet het zoeken in rij 1, kolom 1. Loop één voor één door de rijen totdat een leeg veldje is gevonden. In bovenstaande puzzel (figuur 5) is veldje [1,1] het eerste veldje dat leeg is. Dus laten we daar eens beginnen. - Kies een nieuw cijfer.
Probeer getal "1" als eerste voor vakje [1,1]. - Controleer de rij.
Controleer of het nieuwe getal "1" al voorkomt in rij [1]. Met andere woorden, is het nieuwe getal "1" in veldje [1,1] een legale zet, ja of nee. - Controleer de kolom
Controleer of het nieuwe getal "1" al voorkomt in een kolom [1]. - Controleer het 3x3 veldje
Controleer of het nieuwe getal "1" al voorkomt in het 3x3 veldje [1,1] t/m [3,3]. - Is de zet legaal.
Als op voorgaande vragen driemaal "nee" als antwoord krijg, plaats het getal "1" op locatie [1,1]. Krijg je niet driemaal een "nee", dan is het getal niet mogelijk. Het is niet uniek. Ga dan naar het volgende getal, ga terug naar stap 2 en neem het volgende getal, "2". Doe weer de drie controles en kijk of "2" een legale zet oplevert. Indien nodig loop door de getallen 1 t/m 9. - Plaats het getal.
Als een uniek getal is gevonden voor [1,1], ga dan naar het volgende lege veldje. Ga dus weer terug naar stap 1. Het volgende lege veldje is dan [3,1]. Probeer weer een getal, begin weer met getal "1", Controleer dit (stappen 3 t/m 6). Is de zet legaal, plaats het getal in het lege veldje. Is dit niet het geval zal stap 6 aangeven het volgende getal te proberen, getal "2", "3", enz. - Geen uniek getal gevonden.
Wat als geen van de getallen 1 t/m 9 een legale zet opleveren. Dan moeten we een paar stapjes terug zetten door een uniek getal in voorgaande zetten te veranderen. Is in een voorgaande zet het getal 4 geplaatst, kijk of een ander getal mogelijk is en ga weer verder. Is dit niet mogelijk ga nog een stapje verder terug en wijzig dit getal en kijk opnieuw. Dus begin bij het voorgaande veldje. Kijk naar het volgende getal dat mogelijk is op die locatie. Past niets, ga dan nog een stapje terug.
Zoals in voorgaande stappen is aangegeven is het getal "1" een mogelijke zet voor vlakje [1,1]. In de oplossing (figuur 6) is te zien dat het getal in vlakje [1,1] uiteindelijk 8 is geworden door steeds weer terug te gaan. - Naar de oplossing.
Door voorgaande stappen 1 t/m 8 netjes en gestructureerd te herhalen kan de Sudoku (5) worden opgelost. Figuur 6 geeft de uiteindelijke oplossing.
Er zijn natuurlijk meerdere manieren om een Sudoku op te lossen. Iedereen heeft zo zijn/haar eigen techniek. Zo kun je ook zoeken naar een veldjes waar één cijfer mogelijk is. Vul dit cijfer in en zoek naar het volgende veldje waar maar één oplossing mogelijk is. Zo komen we ook tot een oplossing. We kunnen hiervoor ook gebruik maken van enkele handelingen uit voorgaande strategie. Namelijk het zoeken naar lege veldjes en controleren of een zet legaal is.
De uitgeschreven methode noemen we een algoritme. Met dit algoritme kunnen we de VBA code schrijven. Dit kunnen we stapje voor stapje doen.
Stukjes VBA code
Door voor elke stap apart VBA code op te stellen kun je eenvoudig een heel programma samenstellen. Je kunt elk stukje afzonderlijk testen en volgen. Met deze manier van werken hak je een project, een onderdeel van een project in stukjes. Tip: maak zoveel mogelijk stukjes waarin maar één handeling wordt uitgevoerd.
Voor we starten moeten we eerst nog een paar dingen doen. We moeten nog een veldje maken, de hints vastleggen en de stappen vastleggen. De Sudoku zelf laat al een deel van de oplossing zien, neem voor een veldje een matrix 9x9 (een zogenaamd Array). Plaats de hints in deze matrix, plaats het getal "5" op locatie [1,2], het getal "3" op [1,4] enz. Plaats op de locatie van lege veldjes bijvoorbeeld het getal "0". Misschien heb je nog een matrix 9x9 nodig om de voortgang te monitoren, welke stappen zijn er allemaal gezet.
Met deze gegevens kunnen we beginnen met stap 1; het zoeken naar een leeg veldje.

De volgende stapjes zijn de controles of specifieke zet een legale zet is


En zo gaan we door met het invullen van alle stapjes. Probeer het nu zelf en als het helemaal niet lukt kijk naar de volledige VBA code, ga naar "Sudoku" onder Downloads. Let op, dit is één manier om tot een oplossing te komen. Dit is zeker niet de enige oplossing. Dus de VBA code zal zeker niet aansluiten op de code die je zelf hebt opgesteld. Het belangrijkste is dat je de gekozen oplossing snapt, kunt volgen en probeer het dan nog eens. Oefening baart kunst.
Als je goed kijkt valt één ding op in de voorbeeld VBA code. In de procedure "Solve" wordt de procedure "Solve" opnieuw aangeroepen. Als een procedure/functie zichzelf aanroept heeft dit een speciale naam; "Recursie". Recursie is een erg krachtige manier van programmeren. Deze techniek wordt gebruikt als stappen zich vaak herhalen en van elkaar afhankelijk zijn. Een van de meest gebruikte voorbeelden van het gebruik van Recursie is het berekenen van x! (x faculteit). Google de term "recursie" maar eens.
Recursie is krachtig maar het is tevens ook erg lastig. Je zult zien dat de kans op fouten heel groot is en zogenaamde vastlopers zullen heel vaak volgen. Het is goed om dit in je achterhoofd te houden.

Probeer het eens.....


