Parametrisch ontwerpen

Parametrisch ontwerpen

We doen even een stapje terug; Wat is parametrisch ontwerpen? Als we een Google-search uitvoeren op deze term worden allerlei organische figuren zichtbaar, bijzondere vlakdelingen en repetities van kleinere elementen tot bijzondere vormen. Als we de term “Architectuur” toevoegen veranderd dit beeld niet. Parametrisch ontwerpen lijkt gekoppeld te zijn aan natuurlijke en vloeiende lijnen. De grafische component is hier duidelijk zichtbaar. Is dit parametrisch ontwerpen?

Laten we nog een stap terug nemen en kijken naar het woord “Parametrisch”. Als we dit googelen zien we onder andere de Wikipedia site met veel verwijzingen naar allerlei vakgebieden, allemaal wiskundig van aard. Wolfram MathWorld geeft een definitie voor parametrische vergelijkingen:

Parametric equations are a set of equations that express a set of quantities as explicit functions of a number of independent variables, known as "parameters."

Dit maakt het niet echt veel duidelijker, maar het belangrijkste is dat wiskundige functies altijd parametrisch zijn opgezet. Voor elke parameter kun je zelf een getal (een waarde) invullen en na een berekening volgt er een resultaat gebaseerd op het getallen die zijn ingevuld. Dit concept gaan we in het het navolgende verder volgen.

Parametrisch vergelijkingen

Aan de hand van een eenvoudig voorbeeld wordt duidelijk wat parametrische vergelijkingen zijn en wat de mogelijkheden zijn. Neem een cirkel, deze kunnen we beschrijven met twee functies.

x = r · cos(θ)     en      y = r · sin(θ)

waarin r de straal van de gewenste cirkel en θ (theta) de hoek (in graden of radialen)

Met behulp van de parameters “r” en “θ” kunnen punten (coördinaten) op elke willekeurige cirkel bepalen, hierbij ligt het centrum van de cirkel in de oorsprong (x=0 en y=0). Door de hoek θ verschillende waarden tussen 0 en 360º te geven ontstaan verschillende resultaten voor x en y, de coördinaten van punten op de cirkel. Met de parameter “r” kan de gewenste afmeting, straal van de cirkel worden aangegeven. Door de verschillende punten met elkaar te verbinden kunnen we een cirkel “tekenen”.

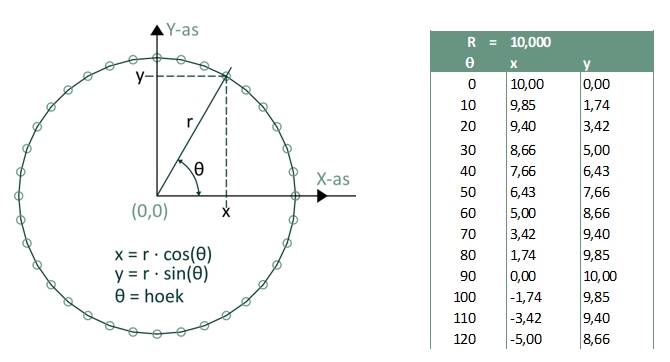
Bovenstaande figuur toont op twee verschillende manieren de resultaten van deze bewerking, de berekening van de x- en y coördinaten voor verschillende waarden van de parameter, de variabele θ (theta) en r. Links een grafische voorstelling en rechts een tabel met getallen. Afhankelijk van de situatie kan voor één of beide voorstellingen worden gekozen als hulp bij het kiezen van de beste set waarden voor het vraagstuk.

Zoals bekend, mensen zijn er visueel ingesteld en daarom kunnen we grafische beelden veel beter beoordelen dan een hele lijst getallen. Grafische beelden geven een sneller en beter beeld van de situatie. Dit kunnen we nog verder verbeteren door de verschillende situaties naast elkaar te plaatsen of snel achter elkaar zichtbaar te maken in een animatie. De gevolgen van veranderingen van de waarde van parameters worden in “real time” zichtbaar. Het visualiseren van verschillende sets van parameters en resultaten kan op heel veel verschillende manieren en is afhankelijk van de situatie. Steeds vaker worden 3D grafische voorstellingen toegepast. Voordelen van dagelijkse toepassingen zal iedereen kunnen benoemen, zoals bijvoorbeeld weerkaarten, navigatie systemen, planning, beurskoersen enz.

Terug naar ons voorbeeld. Naast het wijzigen van de waarde van de parameter/variabele θ, is het ook mogelijk om de functies zelf te wijzigen. Stel dat we de functie voor x wijzigen.

We wijzigen de functie x = r · cos(θ) in  x = θ en we tekenen de resultaten weer ontstaat er een heel andere grafische voorstelling. In plaats van een cirkel zien we de welbekende grafiek van een sinus-functie. Wijzigingen kunnen dus vergaande gevolgen hebben op het resultaat.

Stel we maken een laatste wijziging en dit maal in de functie y. We nemen alleen de absolute waarde van y, y is altijd een positieve waarde heeft tussen 0 en r;  

y = | r · sin(θ) |

De gevolgen voor de resultaten is direct zichtbaar in de grafische voorstellen van de resultaten. Laten we nu deze kennis (functies, parameters en voorwaarden) toepassen in een daadwerkelijk vraagstuk.

We nemen een heel simpel vraagstuk, een eenvoudige vormstudie van een nieuwe woontoren. De woontoren heeft een centrale kern met daar omheen appartementen. De kern wordt beschreven met een cirkel r1 en de gevel van de toren met r2. Het aantal appartementen wordt bepaald door de deling van de cirkel in taartpunten met het gebruik van θ.

Figuur A laat de twee cirkels zien, de basis van de woontoren. De volgende stap (B) is de opdeling van de toren in verschillende appartementen op basis van de hoek θ. C is de volgende stap. waarbij de functie y = | r · sin(θ)| wordt gebruikt voor het genereren van de balkons aan de gevel. Een mogelijke volgende stap (D) is het vervangen van de gevel omsluitende ronde balkons met rechthoekige vormen die wellicht niet de hele gevel omvatten. Voor de eenvoud segmenteren we nog de gevellijn. Dit is gewoon eenvoudiger om te bouwen. Met deze eenvoudige regels, parameters en set functies kan snel een plattegrond worden gegenereerd en een volume. We kunnen het resultaat wederom grafisch weergeven en beoordelen. De grafische voorstelling is een representatieve weergave van de resultaten van de uitgevoerde berekeningen. Presenteer  de verschillende resultaten naast elkaar en we kunnen snel beslissen wat goed is aan een vorm en wat niet. Enkele van de mogelijke resultaten zijn weergegeven in navolgende figuur.

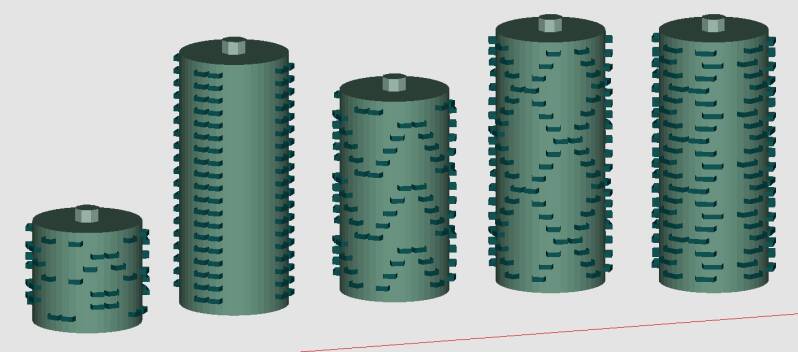
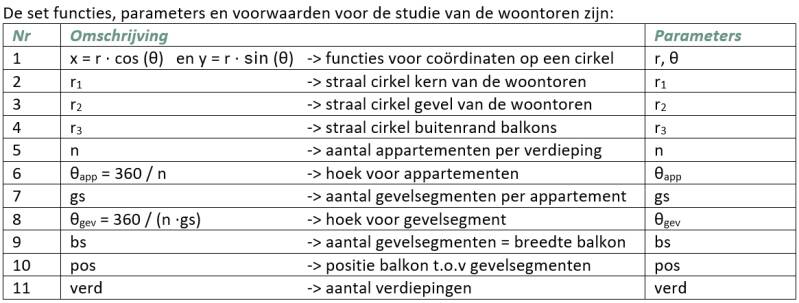
Op basis van enkele eenvoudige voorwaarden, functies en parameters (zie voorgaande set)  kunnen veel resultaten, varianten worden verkregen en kan de beste set waarden voor de parameters worden gekozen.

Natuurlijk is het eenvoudig om de lijst met resultaten naar wens aan te vullen met allerlei aspecten die helpen bij het maken van een juiste beslissing. Zo kan het oppervlak van een appartement worden bepaald, de inhoud van de toren, het aantal elementen, zoals balkons, gewichten en naast constructieve gegevens kunnen kengetallen worden bepaald die helpen bij de toetsingen van eisen en normen, het glasoppervlak, lichtinval, isolatiewaarden in relatie tot het oppervlak van de gevel, enz. Deze gegevens kunnen worden bepaald bij de berekening van iedere set waarden voor de parameters, voor iedere variant. 

Dit voorbeeld is opgebouwd op basis van twee hele eenvoudige functies met enkele parameters en regels. Zoals aangegeven kan deze studieset eenvoudig worden aangevuld met allerlei aanvullende gegevens. Het is ook mogelijk om de parameters en/of functies zelf te wijzigen. Geringe aanpassingen kunnen verrassende resultaten opleveren. Dit is de kracht van parametrisch ontwerpen.

Nog een voorbeeld. Wat gebeurd er als we de functies voor een cirkel vervangen door een andere wiskundige functie, bijvoorbeeld de functie voor een Maurer Rose. De Maurer Rose functie is, evenals de functies voor een cirkel, heel eenvoudig en werkt op exact dezelfde wijze als die van een cirkel. De functies en parameters gebruikt voor een Maurer Rose zijn nagenoeg gelijk aan die van de eerder gegeven sinus- en cosinusfunctie, de resultaten lijken echter helemaal niet op een cirkel. Je kunt zeggen; de resultaten zijn verrassend.

Met deze nieuwe functies zijn we in staat andere vormen (varianten) te genereren voor de woontoren.

Nog een laatste voorbeeld.

Een ander gebruik van de bekende sinus- en cosinusfunctie is weergegeven in navolgende figuren. Hierbij zijn dezelfde rekenresultaten op een andere wijze toegepast. Dit keer zijn de functies met verschillende waarden voor de parameters naast elkaar geplaatst op een plat vlak. Dit resultaat kunnen we mogelijk gebruiken voor het ontwerp van gevelpanelen voor onze woontoren.

Met een kleine aanpassing van de ontwerpvoorwaarden zijn ook hier weer varianten mogelijk.

Parametrisch ontwerp

Voorgaande voorbeelden van het gebruik van parametrische functies met de grafische voorstellingen geven al snel het beeld van een architectonisch ontwerp. Met de grafische component wordt al snel een link gelegd met architectonisch ontwerpen. Het sluit goed aan bij de eerdere voorbeelden uit de zoek actie met Google. Er zijn ook architectonische voorbeelden in Nederland, bijvoorbeeld in Eindhoven.

Waarom is dit gebouw een mooi voorbeeld voor parametrisch ontwerpen? Zonder parametrisch beschouwingen zou dit nooit zijn gebouwd. Het zou veel te duur zijn. Dit brengt ons direct bij een heel belangrijk aspect van parametrisch ontwerpen; het digitaliseren van vormen, van data, van resultaten. In ons voorbeeld zijn we gestart met het formuleren van een wiskundige functie voor de bepaling van x- en y-coördinaten voor een specifieke vorm. Voor verschillende parameters zijn bijbehorende x,y coördinaat berekend en vervolgens is een grafische voorstelling verwerkt. Hiervoor vormen de berekende coördinaten de basis. Dit geldt voor elk parametrisch ontwerp.

Met een parametrische opzet kunnen we elke willekeurig punt in een vorm bepalen, elk punt ligt vast. Dit betekent dat we allerlei gegevens kunnen bepalen op basis van deze punten met bekende x,y coördinaten. Denk aan de afstand tussen twee punten, hoogteverschillen, een oppervlak, een inhoud enz. Allerlei geometrische gegevens van deze rare fluïde vorm zijn bekend. Ze zijn niet altijd even duidelijk, maar ze liggen altijd digitaal vast.

Dit betekent voor de boetiek in Eindhoven dat de vorm van elk gevelpaneel bekend is. Daarmee kunnen we heel eenvoudig alle gevelpanelen produceren, ook al heeft elk paneel een andere vorm en afmeting. Maak een overzicht van de locatie van ieder panelen – een merkenplan – en de vloeiende vorm kan heel eenvoudig worden gebouwd.

Door de digitalisering wordt het eenvoudig om bijzondere vormen te produceren. Allerlei fabricageprocessen zijn immers al gedigitaliseerd en kunnen met de juiste input nagenoeg elke willekeurig voorwerp genereren en/of produceren. Denk aan allerlei CNC-machines, robots, 3D printers enz. Al deze technieken vinden hun weg naar de bouw en openen een hele nieuwe wereld voor ons bouwers én voor ons constructeurs.

Enkele overwegingen

Parametrische vormen

De uitleg richt zich heel sterk op een grafische vorm, maar zoals aangegeven is een uitvoer van getallen in een tabel ook mogelijk. Allerlei varianten voor in- en uitvoer zijn mogelijk. Dit geldt ook voor het soort vraagstuk. Parametrisch ontwerpen blijft zeker niet beperkt tot architectonische vormen. Alle vraagstukken kan men formuleren in een studie met parameters, zoals optimalisatie vraagstukken, planning, kosten, sterkte en stijfheid beschouwingen. Onze rekensoftware is immers ook een tool waarin gebruik wordt gemaakt van parameters, zoals de lengte van een balk, de doorsnede van een balk, de belastingen en de belastingcombinaties enz. Hier rolt een resultaat uit en we beoordelen dit. Is het niet naar wens, passen we de waarde van enkele parameters aan om een resultaat te genereren dat voldoet aan onze wensen.

Wat we misschien niet zo vaak doen is het “automatisch” genereren van heel veel verschillende resultaten om daaruit de beste te kiezen. Voor ons constructeurs blijft dit vaak beperkt tot het “spelen” met enkele belastingen, een afmeting, een hoeveelheid wapening of de wanddikte van een staalprofiel. Hoewel er gebruik wordt gemaakt van “parametrische modellen”, is dit (denk ik) niet de gedachte van parametrisch ontwerpen. Het spelen met parameters, voorwaarden en resultaten is daadwerkelijk parametrisch ontwerpen. Dit is het “ontwerpspel”. Het levert gegarandeerd ook veel meer mogelijkheden op én betere resultaten.

Vastleggen van functies, parameters en voorwaarden

Voor de vormstudie van de woontoren is gebruik gemaakt van twee eenvoudige wiskundige goniometrische functies. Er zijn verschillende parameters benoemd, parameters die van belang zijn voor het vraagstuk. Parameters die bepalend zijn voor een vraagstuk. Deze zijn niet altijd even evident, daarom start altijd met enkele voor de hand liggende parameters en voeg later nieuwe toe. Door parameters toe te voegen neemt de complexiteit toe en deze geleidelijke aanpak resulteert in een goed overzicht.

Het hele proces van het formuleren van een vraagstuk, parameters en voorwaarden is de eerste stap in het proces van parametrisch ontwerpen. De volgende stap is het digitaliseren van het vraagstuk. Daarvoor wordt ALTIJD gebruik gemaakt van software en/of programmeren. Dit kan in de vorm van een eenvoudig berekening met een rekenmachine, een spreadsheet, het formuleren van componenten (families) of een computerprogramma (in een willekeurige computertaal, waaronder ook visual programming).

Er komt ALTIJD een moment dat we het vraagstuk in een computer moeten invoeren. Hiervoor is altijd een stukje programma noodzakelijk, in welke vorm dan ook. Zoals het invoeren van functies in een spreadsheet of een ander (grafisch) computerprogramma. Vandaag de dag wordt door ons veel gebruik gemaakt van commerciële software zoals grafische pakketten als Revit en Tekla (er zijn overigens nog veel meer voorbeelden). Deze kunnen we gebruiken voor parametrisch ontwerpen / studies. Andere voorbeelden zijn pakketten als Dynamo en Grasshopper. Dit zijn visuele programmeertalen die direct gekoppeld zijn aan grafische pakketten, zoals Revit en Tekla.  De gemene deler is hier het digitalisering van het vraagstuk in een programma – in welke vorm dan ook.

Bedankt dat elk computerprogramma in de wereld een parametrisch systeem is. Zonder parameters werkt een programma simpelweg niet.

Ontwikkeling in gaming

Een van de belangrijkste ontwikkelingen die verantwoordelijk zijn voor de trends die we waarnemen in de bouw is voor een groot deel terug te voeren naar de gaming industrie. Het visualiseren van onze wereld en denkbeeldige werelden, het digitaliseren eervan is een van de belangrijkste onderdelen van gaming. Deze gigantische industrie is verantwoordelijk voor heel veel ontwikkellingen op het gebied van grafische software, visualisatie technieken en hardware zoals CPU’s en GPU’s. Al deze ontwikkelingen worden nu toegepast in pakketten als Revit en Tekla. Andere handigheidjes, zoals visual programing, komt ook uit deze industrie. Games moeten immers steeds sneller worden geproduceerd terwijl de games steeds complexer en steeds gedetailleerder worden. De gamer van tegenwoordig wil namelijk in FIFA ieder grassprietje van de grasmat apart zien bewegen op zijn scherm, iedere gamer wil in GTA alle botsing van auto’s zo natuurgetrouw mogelijk op zijn scherm hebben. Dit vraagt heel veel van digitalisering, rekentechnieken en visualisering. Daar maken we steeds meer gebruik van. Van deze industrie kunnen we nog heel veel leren.

Spelen met constructies

Een van de belangrijkste eigenschappen van parametrisch ontwerpen en parametrische vraagstukken is het genereren van heel veel verschillende varianten in een korte tijd. Dit geeft de mogelijkheid om met deze resultaten te spelen. Parametrisch ontwerpen is spelen met digitale data. Stel daarom bij elke vraagstuk steeds weer opnieuw de vraag: Wat gebeurd er als ik dit of dat verander? Dit spelen met de vraagstukken is eigenlijk de magie van parametrisch ontwerpen.

Het "spelen" met constructies kan zo (weer) een onderdeel worden van ons dagelijks werk. Dit is niet altijd even makkelijk en het zal wat oefening vragen, maar de resultaten zullen zeker bijzonder zijn.

Nieuwe vormen

Parametrisch ontwerpen en bijzondere vormen hebben een sterke relatie met elkaar. Dit vinden we ook steeds meer terug in parametrische gebouwen, zeker als productietechnieken zoals 3D printen steeds beter en sneller worden. Het is niet de vraag of dit gaat gebeuren, het is alleen een kwestie van tijd. Binnen tien jaar zal onze wereld zeker heel anders zijn. Om een indruk te krijgen google in de tussentijd eens de volgende zoektermen:

• “Zaha Hadid”
• “Parametric Architecture”
• “IwamotoScott Architecture”
• “Parametric structural design”

of bezoek eens de volgende links.

https://www.zaha-hadid.com/

https://www.youtube.com/watch?v=MrRvX5I8PyY/

https://en.wikipedia.org/wiki/Grasshopper_3D/

https://dynamobim.org/

Have fun en bij het zien van alle mooie beelden, gebouwen en technieken. Dan wordt zeker snel duidelijk dat de bouwwereld en de wereld van een constructeur heel anders gaat worden.

Tot slot nog een voorbeeld

Van de gebruikte voorbeelden is een spreadsheet opgesteld met wat programmeerwerk (VBA). Dit geeft de mogelijkheid om eens zelf te spelen met de vormstudies. Dit geeft de mogelijkheid om eigen vraagstukken te formuleren en toe te passen.

Het is niet direct nodig om dure software aan te schaffen om parametrische ontwerpen te maken. Het gebruik van bekende technieken, tools en software is prima mogelijk. Onder downloads is de betreffende spreadsheet terug te vinden en er zullen er op een later tijdstip nog meer voorbeelden volgen voor inspiratie. Probeer het eens.